Directional limits on persistent gravitational waves from Advanced LIGO's first observing run
Notebook to re-create plots from the publication available at arXiv:1612.02030
Contents
General Definitions
% define power law index values alpha = [0 2 3]; % strings for printing units str1 = '[strain^2 Hz^{-1}]'; str2 = '[strain^2 Hz^{-1} sr^{-1}]'; ergs1 = '[ergs cm^{-2} s^{-1} Hz^{-1}]'; ergs2 = '[ergs cm^{-2} s^{-1} Hz^{-1} sr^{-1}]';
Figure 1 - Braodband Radiometer (BBR) skymaps
% Plot SNR maps for a = 1:length(alpha); astr(a) = num2str(alpha(a)); % correct numeric value for alpha = 2/3 alph = alpha(a); switch alph case 2 alph = 2/3; %fprintf('set alpha = %0.2f\n',alph) otherwise %fprintf('leave alpha = %0.2f\n',alph) end % load in data from data files radstr = ['fig1_bbr_a' astr(a)]; raddat = load([radstr '.dat']); radmat.snr = raddat(:,1); % plot SNR maps plotMapAitoff(radmat.snr,360,181,-1); % snr plot colorbar('FontSize',25); set(gcf,'renderer', 'zbuffer'); set(gca, 'position', [0.12 0.15 .76 1]); print('-dpng',['fig1_bbr_SNR_a' astr(a) '.png']); title(['BBR SNR Map, \alpha=' num2str(alph)], 'FontSize', 14); end % Plot upper limit maps for a = 1:length(alpha); astr(a) = num2str(alpha(a)); % correct numeric value for alpha = 2/3 alph = alpha(a); switch alph case 2 alph = 2/3; %fprintf('set alpha = %0.2f\n',alph) otherwise %fprintf('leave alpha = %0.2f\n',alph) end % load in data from data files radstr = ['fig1_bbr_a' astr(a)]; raddat = load([radstr '.dat']); radmat.ul_flux = raddat(:,2); %plot UL flux map plotMapAitoff(radmat.ul_flux,360,181,-1); % flux upper limit map colorbar('FontSize',25); set(gcf,'renderer', 'zbuffer'); set(gca, 'position', [0.1 0.15 .7 1]); print('-dpng',['fig1_bbr_UL_a' astr(a) '.png']); title(['BBR flux UL Map, \alpha=' num2str(alph)], 'FontSize', 14); end
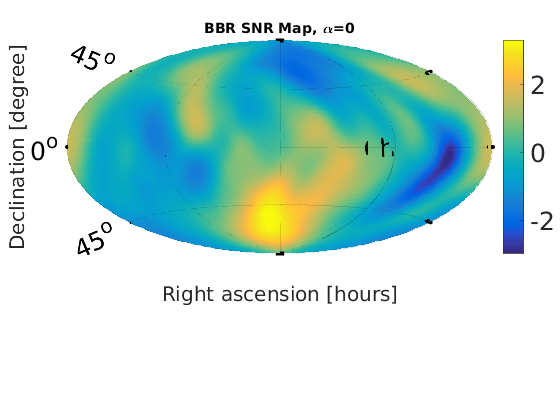
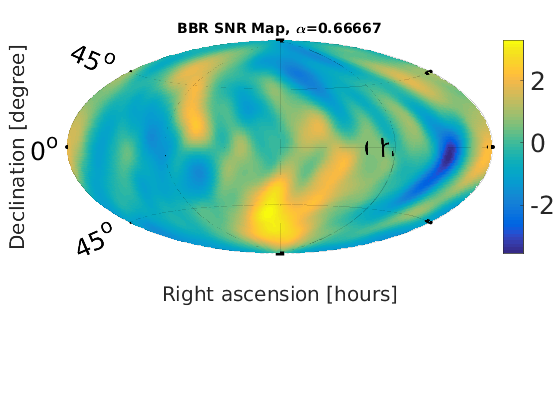
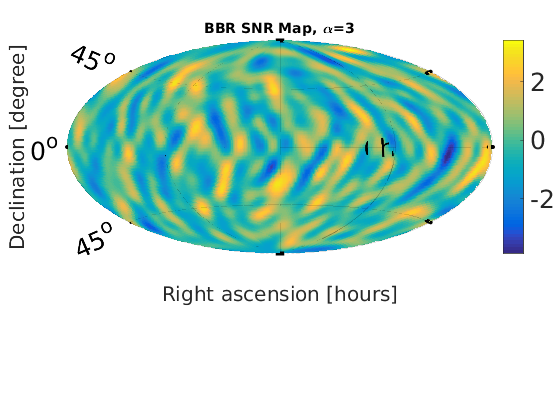
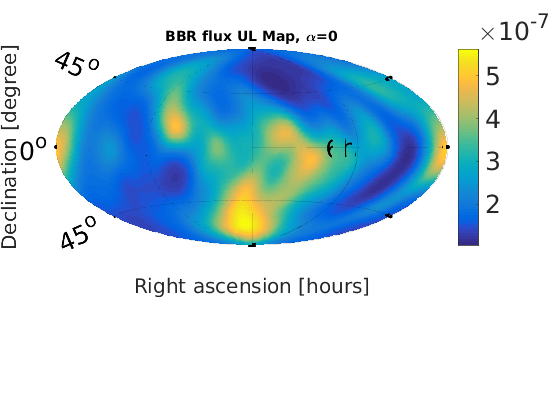
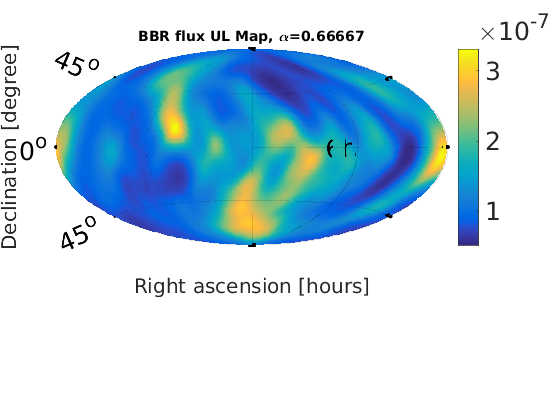
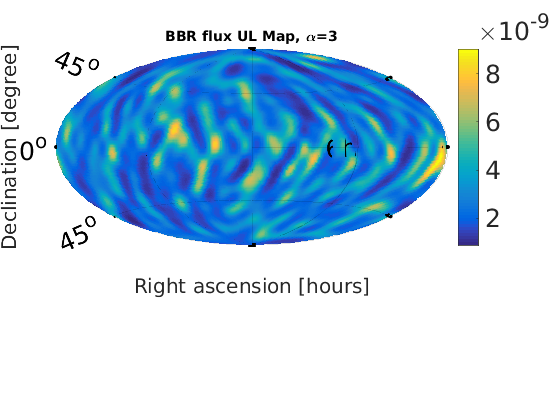
Figure 2 - Spherical Harmonic Decomposition (SHD) skymaps
% Plot SNR maps for a = 1:length(alpha); astr(a) = num2str(alpha(a)); % correct numeric value for alpha = 2/3 alph = alpha(a); switch alph case 2 alph = 2/3; %fprintf('set alpha = %0.2f\n',alph) otherwise %fprintf('leave alpha = %0.2f\n',alph) end % load in data from data files sphstr = ['fig2_shd_a' astr(a)]; sphdat = load([sphstr '.dat']); sphmat.snr = sphdat(:,1); % plot SNR map plotMapAitoff(sphmat.snr,360,181,-1); % SNR plot colorbar('FontSize',25); set(gcf,'renderer', 'zbuffer'); set(gca, 'position', [0.12 0.15 .76 1]); print('-dpng',['fig2_shd_SNR_a' astr(a) '.png']); title(['SHD SNR map, $\alpha$=', num2str(alph)], 'FontSize', 14); end % Plot upper limit maps for a = 1:length(alpha); astr(a) = num2str(alpha(a)); % correct numeric value for alpha = 2/3 alph = alpha(a); switch alph case 2 alph = 2/3; %fprintf('set alpha = %0.2f\n',alph) otherwise %fprintf('leave alpha = %0.2f\n',alph) end % load in data from data files sphstr = ['fig2_shd_a' astr(a)]; sphdat = load([sphstr '.dat']); sphmat.ul_omega = sphdat(:,2); % plot omega UL map plotMapAitoff(sphmat.ul_omega,360,181,-1); % energy density upper limit plot colorbar('FontSize',25); set(gcf,'renderer', 'zbuffer'); set(gca, 'position', [0.1 0.15 .7 1]); print('-dpng',['fig2_shd_UL_a' astr(a) '.png']); title(['SHD UL map \alpha=', num2str(alph)], 'FontSize', 14); end
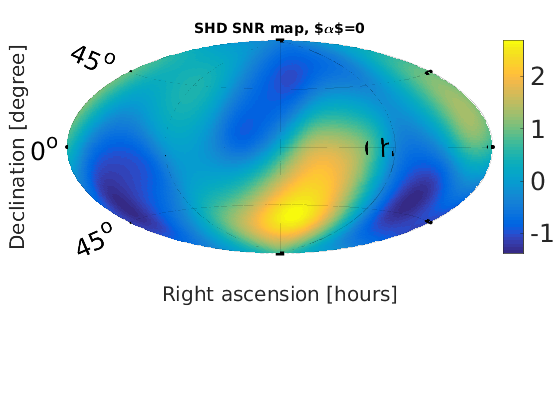
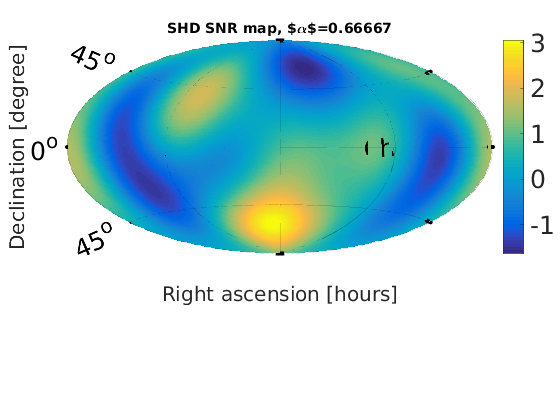
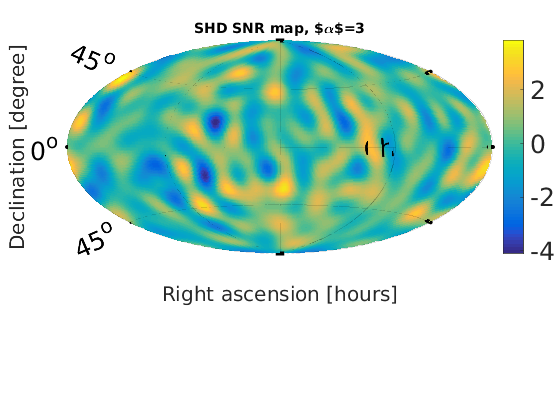
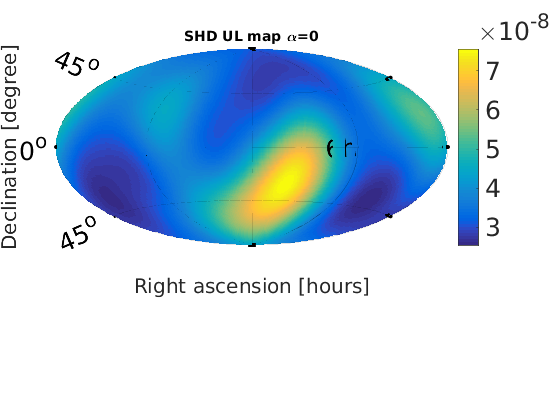
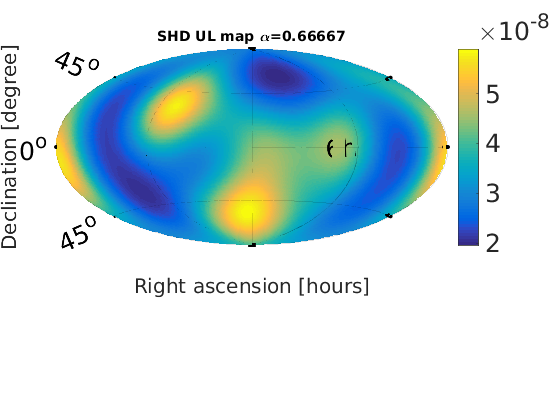
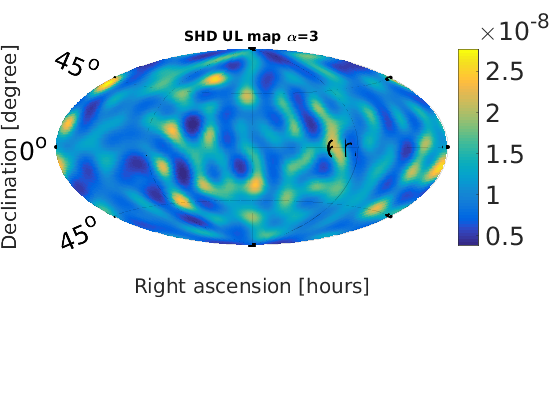
Figure 3 - Angular power (Cl) upper limits
matstr1 = 'fig3_Cls_a'; matstr2 = '.dat'; matstr3 = '.mat'; % load a0 and a3 data for limits cl0 = load([matstr1 '0' matstr3]); cl3 = load([matstr1 '3' matstr3]); % define draw arrow function drawArrow = @(x,y,varargin) quiver( x(1),y(1),x(2)-x(1),y(2)-y(1),0, varargin{:} ); % start figure figure('units','normalized','position',[0 0 1 .3]) % load alpha = 0 a=1; clstr = [matstr1 astr(a)]; load([clstr matstr3]); cldat = load([clstr matstr2]); clear('x1'); x1 = cldat(:,1); clear('y1'); y1 = cldat(:,2); % plot alpha = 0 p0 = semilogy(x1, y1,'o', 'MarkerSize', 10); hold on; % draw upper limit arrow for each l for j=1:length(y1) drawArrow([x1(j) x1(j)], [cl3.y0(j) y1(j)], 'kv', 'MarkerFaceColor', p0.Color) end % load alpha = 2/3 data a=2; clstr = [matstr1 astr(a)]; load([clstr matstr3]); cldat = load([clstr matstr2]); clear('x1'); x1 = cldat(:,1); clear('y1'); y1 = cldat(:,2); % plot alpha = 2/3 data p2 = semilogy(x1, y1,'o', 'MarkerSize', 10, 'Color', [0.8500 0.3250 0.0980]); hold on; % draw upper limit arrow for each l for j=1:length(y1) drawArrow([x1(j) x1(j)], [cl3.y0(j) y1(j)], 'kv', 'MarkerFaceColor', p2.Color) end % load alpha = 3 data a=3; clstr = [matstr1 astr(a)]; load([clstr matstr3]); cldat = load([clstr matstr2]); clear('x1'); x1 = cldat(:,1); clear('y1'); y1 = cldat(:,2); % plot alpha = 3 data p3 = semilogy(x1, y1,'o', 'MarkerSize', 10); hold on; % draw upper limit arrow for each l for j=1:length(y1) drawArrow([x1(j) x1(j)], [cl3.y0(j) y1(j)], 'kv', 'MarkerFaceColor', 'w') ;%p3.Color) end % set axis limits and labels xlim([-0.5 xmax+0.5]); ylim([ymin ymax]); ylim([cl3.ymin cl0.ymax]); grid on xlabel('$l$', 'Interpreter','latex','FontSize',34); %ylabel('$C_l^{1/2}$ [Energy Density]', 'Interpreter','latex','FontSize',28); ylabel('$C_l^{1/2}$ [$\Omega_{gw}$ sr${}^{-1}$]', 'Interpreter','latex', 'FontSize',34); %set(gca, 'OuterPosition', [0 0 1 1]); pretty2(32,20); fig=gcf; %fig.PaperUnits = 'normalized'; fig.PaperPosition = [0 0 .9 .6]; fig.PaperUnits = 'inches'; fig.PaperPosition = [0 0 15 5]; % set legend legend([p0 p2 p3], '\alpha=0', '\alpha=^2/_3', '\alpha=3') legend('BoxOff') % save to file print('-dpng', ['fig3_ClULs.png'], '-r0');
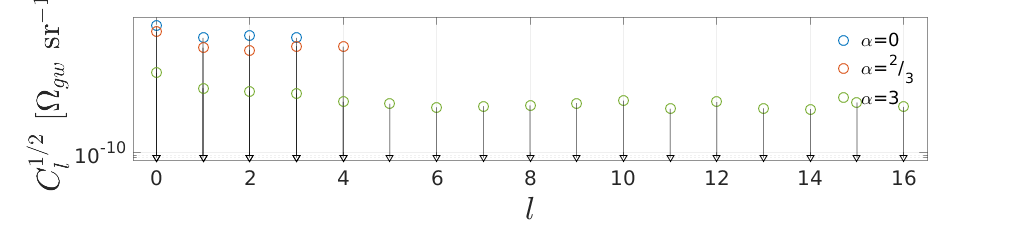
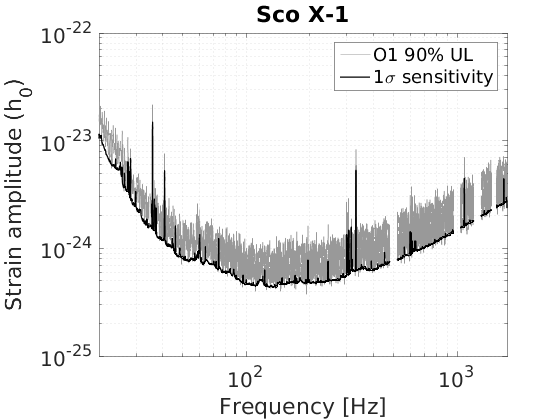
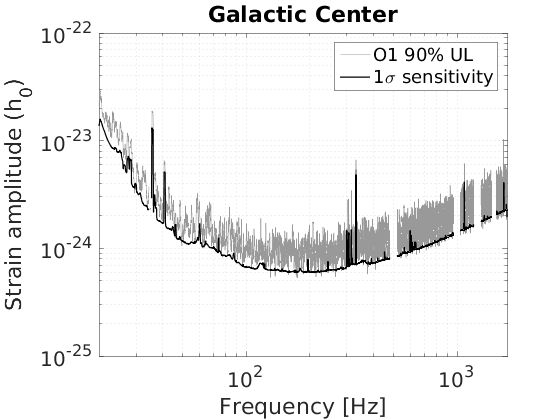
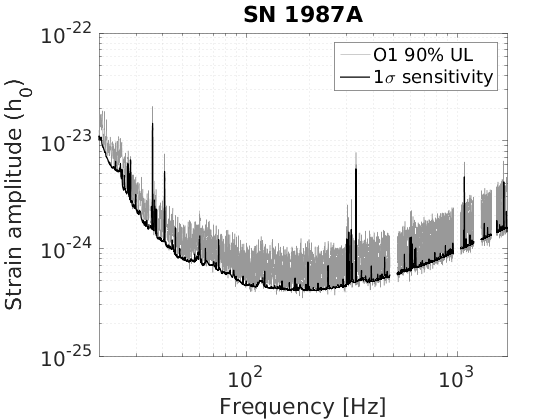
Figure 4 - Narrowband Radiometer (NBR) upper limits
matstr = 'fig4_nbr_'; % Scorpius X-1 nbstr = 'sco'; clear('nbdat'); nbdat = load([matstr nbstr '.dat']); nbmat.f = nbdat(:,1); nbmat.ul = nbdat(:,2); nbmat.one_sigma = nbdat(:,3); nbmat.conf = 0.9; % make strain amplitude UL plot figure; %('units','normalized','position',[0 0 1 0.3]); loglog(nbmat.f, nbmat.ul,'Color',[0.6 0.6 0.6]); hold on; loglog(nbmat.f, nbmat.one_sigma,'k','LineWidth', 1.2); pretty; grid minor; xlabel('Frequency [Hz]'); ylabel('Strain amplitude (h_0)'); title('Sco X-1'); legend({['O1 ' num2str((nbmat.conf)*100) '% UL'], '1\sigma sensitivity'}); xlim([min(nbmat.f),max(nbmat.f)]); print('-dpng',['fig4_' nbstr]); % Galactic Center nbstr = 'gc'; clear('nbdat'); nbdat = load([matstr nbstr '.dat']); nbmat.f = nbdat(:,1); nbmat.ul = nbdat(:,2); nbmat.one_sigma=nbdat(:,3); nbmat.conf = 0.9; % make strain amplitude UL plot figure; %('units','normalized','position',[0 0 1 0.3]); loglog(nbmat.f, nbmat.ul,'Color',[0.6 0.6 0.6]); hold on; loglog(nbmat.f, nbmat.one_sigma,'k','LineWidth', 1.2); pretty; grid minor; xlabel('Frequency [Hz]'); ylabel('Strain amplitude (h_0)'); title('Galactic Center'); legend({['O1 ' num2str((nbmat.conf)*100) '% UL'], '1\sigma sensitivity'}); xlim([min(nbmat.f),max(nbmat.f)]); print('-dpng',['fig4_' nbstr]); % Supernova 1987A nbstr = 'sn'; clear('nbdat'); nbdat = load([matstr nbstr '.dat']); nbmat.f = nbdat(:,1); nbmat.ul = nbdat(:,2); nbmat.one_sigma=nbdat(:,3); nbmat.conf = 0.9; % make strain amplitude UL plot figure; %('units','normalized','position',[0 0 1 0.3]); loglog(nbmat.f, nbmat.ul,'Color',[0.6 0.6 0.6]); hold on; loglog(nbmat.f, nbmat.one_sigma,'k','LineWidth', 1.2); pretty; grid minor; xlabel('Frequency [Hz]'); ylabel('Strain amplitude (h_0)'); title('SN 1987A'); legend({['O1 ' num2str((nbmat.conf)*100) '% UL'], '1\sigma sensitivity'}); xlim([min(nbmat.f),max(nbmat.f)]); print('-dpng',['fig4_' nbstr]);